Основы алгебры логики
| 1.4. Основы алгебры логики
Алгебра логики (АЛ) является основным инструментом синтеза и анализа дискретных автоматов всех уровней. АЛ называют также Булевой алгеброй. АЛ базируется на трёх функциях, определяющих три основные логические операции. 1. Функция отрицания (НЕ). f1 =`X читается, как f1 есть (эквивалентна) НЕ Х. Элемент, реализующий функцию НЕ, называется элементом НЕ (инвертором).
2. Функция логического умножения (конъюнкции). Функция логического умножения записывается в виде f2=X1·X2. Символы логического умножения &, L, <×>, ´. Функция конъюнкции читается так: f2 есть (эквивалентна) Х1 и Х2, поскольку функция истинна тогда, когда истинны 1-й и 2-й аргументы (переменные). Конъюнкцию называют функцией И, элемент, реализующий эту функцию, элементом И.

В общем случае функцию логического умножения от n переменных записывают так:

Количество переменных (аргументов), участвующих в одной конъюнкции, соответствует количеству входов элемента И. 3. Логическое сложение (дизъюнкция). Функция логического сложения записывается в виде f3=X1 + X2, и читается так: f3 есть Х1 или Х2, поскольку функция истинна, когда истинна одна или другая переменная (хотя бы одна). Поэтому функцию дизъюнкции часто называют функцией ИЛИ. Символы логического сложения +,V. В общем случае функция ИЛИ записывается:

Используя операции (функции) И, ИЛИ, НЕ можно описать поведение любого комбинационного устройства, задав сколь угодно сложное булево выражение. Любое булево выражение состоит из булевых констант и переменных, связанных операциями И, ИЛИ, НЕ. Пример булева выражения:

Основные законы алгебры логики. Основные законы АЛ позволяют проводить эквивалентные преобразования функций, записанных с помощью операций И, ИЛИ, НЕ, приводить их к удобному для дальнейшего использования виду и упрощать запись. ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ Таблица 1.1
Используя законы алгебры логики, можно упростить булевы выражения, в частности, правило склеивания позволяет упростить выражение типа  Действительно, используя законы 2, 5 и 11 можно записать исходное выражение в виде Х2(Х1 +`Х1 ) =Х2. Так как логическая операция Х1 +`Х1 = 1 (см. з-н 5), а Х2×1 = Х2 (см. з-н 2б), полученное выражение истинно. Способы задания функций алгебры логики. При сопоставлении функций АЛ с дискретными автоматами аргументы функций, сопоставляются с входами, а сами функции с выходами дискретного автомата. Поскольку дискретный автомат имеет конечное число входов, то мы будем иметь дело с функцией конечного числа аргументов. Если автомат имеет m входов, то количество входных переменных тоже m и число возможных комбинаций наборов значений этих входных аргументов (переменных) К=2m. Поскольку автомат имеет конечное число входов, его состояние описывается конечным числом значений функций выходов. Существует несколько способов задания функций АЛ и дискретного автомата. 1. Табличный способ. При этом способе функция задается в виде таблицы истинности, представляющей собой совокупность всех наборов переменных и соответствующих им значений функции. Таблица истинности содержит 2m строк, m столбцов (по количеству входов) и один столбец для записи значения функции. Например: пусть требуется задать функцию трех переменных F1(Х1,Х2,Х3) (рис. 1.4), т.е. автомат на три входа и на один выход, следовательно, M=3, К=8.
Следующий способ задания дискретного автомата – числовой. В Этом случае функция задается в виде десятичных эквивалентов номеров наборов аргументов, при которых функция принимает единичное значение. Например, для рассмотренного выше примера функция F1 принимает единичные значения на наборах переменных со следующими номерами: 1, 2, 5, тогда числовой способ задания будет иметь вид  Координатный способ. При этом способе дискретный автомат задается с помощью карты его состояния, которая известна как карта Карно. Карта Карно содержит 2m клеток по числу наборов значений переменных. Каждая клетка определяется координатами строк и столбцов, соответствующими определенному набору переменных. Все входные переменные разбиваются на 2 группы так, что одна группа определяет координаты строк, а другая - координаты столбцов. В каждой клетке карты Карно проставляется соответствующее значение функции на заданном наборе. Пример задания функции трех переменных приведен на рис. 1.5. Числовое выражение этой функции выглядит так:
 Пусть функция задана в числовой форме и имеет вид:  следовательно, К=16, m=4. Сначала проводим разметку координат карты Карно без указания значений функции. Для удобства воспользуемся указанием "шапки" в виде прямых линий, “под” которыми переменные входят в значение координат без отрицания (рис.1.6). Таким образом, по столбцам и по строкам переменные входят без отрицания в пределах линии-шапки.
Для наглядности координаты клеток карты Карно указаны в трех формах: в виде наборов переменных; в виде двоичного числа, соответствующего порядковому номеру набора переменных; в десятичном эквиваленте номеров наборов переменных. На практике координаты внутри клеток не записывают (рис. 1.7), в клетках указываются единичные значения функции, соответствующие “координатным” наборам переменных. Нулевые значения функции в клетки можно не записывать, т.е. клетки, координаты которых определяются наборами переменных с нулевыми значениями функции, можно оставить пустыми. 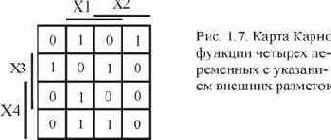 Следует отметить, что перестановка местами переменных Х1 и Х2, а так же переменных Х3 и Х4 допускается, допускается также перестановка местами переменных Х1Х2 и Х4Х3. При построении карты Карно, т.е. при задании логической функции, указывают лишь внешние элементы разметки координат (рис. 1.7). Аналитический способ задания функции алгебры логики. При этом способе функция задается в виде аналитического выражения, полученного путем применения каких-либо логических операций. Например:  Совершенная нормальная дизъюнктивная форма (СНДФ). По таблице истинности можно составить логическое выражение, содержащее наборы переменных, в которые входят все переменные с отрицанием или без. Одна из его форм называется СНДФ. В качестве примера получения СНДФ рассмотрим случай задания логической функции в виде таблицы истинности. Пусть задана функция трех переменных. Таблица истинности этой функции показана на рис. 1.8. (очевидно, что значения функции взяты произвольно и могут быть любыми).
Из таблицы истинности видно, что функция принимает значение логической единицы только на трех наборах переменных, т.е. на 2, 4 и 5-м наборах. Для второй строки (второго набора переменных) можно записать: Х1=0, Х2=1, Х3=0, следовательно, функция f(0,1,0)=1. Принято (по умолчанию) считать, что если переменная в "нормальном" состоянии имеет значение логической единицы, а в инверсном - логического нуля, тогда функцию для второй строки можно представить в виде `X1Х2X3 = 1. Для четвертой строки - `X1X2Х3 = 1 и для пятой строки - Х1X2Х3 = 1. Аналитическое выражение функции выглядит как  Каждое произведение содержит все три переменные с отрицанием или без отрицания и соответствует только одной строке набора переменных, на котором функция принимает значение логической единицы. Произведения, в которых содержатся все переменные с отрицанием или без, называются конституентами единицы или минтермами. Функция будет представлять логическую сумму всех произведений, равных логической единице. В нашем примере вся сумма (дизъюнкция) соответствует совокупности произведений переменных для трех строк. СНДФ любой функции записывается по таблице истинности согласно следующему правилу. Для каждого набора переменных, на которых функция принимает значение логической 1, записываются конституенты, и все эти конституенты объединяются дизъюнктивно. Переменные каждой строки, имеющие значение логического 0, в конституенты входят с отрицанием (записываются в произведение в инвертированном виде), а переменные, имеющие значения логической 1 - без отрицания. Любую логическую (булеву) функцию можно представить дизъюнкцией конституент. Если одно из произведений не содержит хотя бы одной переменной, то такая форма называется нормальной дизъюнктивной формой (НДФ). Например:  Совершенная нормальная конъюнктивная форма (СНКФ). СНКФ можно построить по таблице истинности также как СНДФ. Для чего все значения функции представляют в инверсном виде и записывают СНДФ для инверсной функции. Далее, используя закон де Моргана, получают конъюнкцию всех дизъюнкций. В каждую дизъюнкцию входят все переменные строки таблицы, для которой функция до инвертирования принимала значение логической 1. Если (хотя бы одна) дизъюнкции, которые называются также макстермами (конституентами нуля), не содержат отдельные переменные, то такая форма записи функции называется нормальной конъюнктивной формой (НКФ). Пример записи СНКФ. Пусть функция представлена в виде таблицы истинности (рис. 1.9).
Элементарные функции алгебры-логики. Среди всех функций алгебры логики особое место занимают функции одной и двух переменных, называемые элементарными. В качестве логических операций над переменными, эти функции позволяют реализовать различные функции от любого числа переменных. Общее количество функций АЛ от m переменных R=2k, где k=2m. Рассмотрим элементарные функции от двух переменных
|


















